シャミアの秘密分散法で秘密のデータを分割管理する

つい最近PollyPassHashという新しいパスワード管理手法を知りました。
PolyPassHashingについては時間があれば別のポストで書きますが、要約すると、ある一定数の管理者の正しいパスワードが入力されないと暗号化されたパスワードデータベースを復号化できないようにするための仕組みです。
このポストではPolyPassHashingの中核の暗号技術である シャミアの秘密分散法 の紹介とそれを実現する数学的な仕組みを解説したいと思います。
この記事の内容
シャミアの秘密分散法とはなにか
用語
実際にやってみる: Rubyでシャミアの秘密分散
仕組み
シャミアの秘密分散法とはなにか
名前からわかるとおり、シャミアの秘密分散法はRSAのアルゴリズムにも貢献した有名なイスラエル人の暗号研究者アディ・シャミアによって作られました。
シャミアの秘密分散法は秘密のデータであるシークレットを複数のシェアに分割します。一定数のシェアを持ち寄ることで元のデータを復元することができます。
何かデータを暗号化しなければいけないとしましょう。どんな暗号化方式を使ってもいいですが、暗号の鍵はあとで復号するためにどこかに保存しなければいけません。
この鍵は安全な場所と方法で保管されないといけません。もし、この鍵が盗まれたら攻撃者は暗号化したデータを簡単に復号化できてしまいます。しかし、鍵を安全に保管するというのはとても難しい問題です。その鍵を誰かと共有する場合はもっと難しくなります。
鍵の保管と共有は管理者にとって常に頭痛のタネです。
しかし、シャミアの秘密分散法を使えば二つの問題をかなりの割合で解決することができます。
まず、暗号の鍵を複数に分割してそれぞれを別々の管理者に渡します。各管理者は渡された鍵の断片を大切に保管しなければいけませんが、仮に一つの断片が盗まれたとしても元の鍵は復元することはできません。
攻撃者は複数の管理者が持っている断片を盗まないといけないので、もとの鍵を盗むことは格段に難しくなります。
用語
詳細に行く前に使われる用語を明確にしておきましょう。
シークレット
シークレットは攻撃者には知られてはいけないデータです。メッセージや数字の羅列の形を取り、用途は暗号の鍵だったり秘密にしたいメッセージだったりします。 (英語だとSecretと簡潔に言えますが、日本語でピンとくる単語が見つからなかったのでカタカナにしました。)
シェア
シークレットを分割してできた各断片をシェアと呼びます。シェアはシークレットから計算して得られます。シークレットを復元するためには一定数のシェアがそろわないといけません。(シェアは英語だとshareです。直訳すると割り符になりますが、これもなんかしっくりこないのでシェアと書くことにします。)
閾値
閾値はシークレットを復元するために最低必要なシェアの数です。閾値以上のシェアがそろっている場合のみ、もとのシークレットを復元することができます。
実際にやってみる: Rubyでシャミアの秘密分散
そろそろシャミアの秘密分散が動くところを実際に見てみましょう。僕が書いた小さなRubyのライブラリを使ってデモします。このライブラリはPolyPassHash projectで使われているPythonで書かれたものをポートしたものです。Python版はJustinCapposによって書かれました。
まず、コードをPolyPassHash-Rubyから落としてきて、shamirsecret.rbをirbセッションにロードします。
$ git clone https://github.com/PolyPassHash/PolyPassHash-Ruby
$ cd PolyPassHash-Ruby
$ irb -r ./shamirsecret.rb
実際に秘密のメッセージIn the name of Adi Shamirを分割して、閾値の数のシェアを使うことで復元できることを見てみましょう。
# まず、ShamirSecretクラスのインスタンスを作成しましょう
# 第一引数に閾値の数を渡します。以下の場合だと2が閾値なので、2つ以上のシェアが必要ということになります
# 第二引数には分割したいシークレットを渡します
shamirsecret = ShamirSecret.new(2, "In the name of Adi Shamir")
# 次に与えられたシークレットからシェアを計算します。ここでは3人にシェアを渡すことにしましょう。3つシェアを生成します
# 引数にはシェア番号を渡します。シェア番号が何かは後で説明するので、ここでは一意な整数とだけ覚えておいてください
s1 = shamirsecret.compute_share(1)
s2 = shamirsecret.compute_share(2)
s3 = shamirsecret.compute_share(3)
# シェアを計算したら、シークレットは捨てます。シェアがそろえば復元できるので保管する必要はありません
shamirsecret = nil
# 今度は復元です。もう一度ShamirSecretクラスのインスタンスを作成します。今回は復元なのでシークレットは引数に渡しません
shamirsecret = ShamirSecret.new(2)
# 閾値は2に設定したので2つのシェアがあればシークレットを復元できます
shamirsecret.recover_secretdata([s1,s3])
=> "In the name of Adi Shamir"
今度は正しくないシェアを使ったらどうなるかを見てみましょう。
# 同じようにインスタンスを作成してシェアを計算します
shamirsecret = ShamirSecret.new(2, "In the name of Adi Shamir")
s1 = shamirsecret.compute_share(1)
s2 = shamirsecret.compute_share(2)
s3 = shamirsecret.compute_share(3)
# この時点ではシェアが正しいものであることを確認します
shamirsecret.is_valid_share(s1)
=> true
# シェアの1バイトを変更します
s1[1][0] = s1[1][0] + 1 % 256
# このシェアはもう正しくありません
shamirsecret.is_valid_share(s1)
=> false
# 正しくないシェアを使って復元されたシークレットは壊れています
shamirsecret = nil
shamirsecret = ShamirSecret.new(2)
shamirsecret.recover_secretdata([s1,s3])
=> "\xC6n the name of Adi Shamir"
仕組み
少しだけ数学を勉強しましょう。シャミアの秘密分散法は基礎的な多項式を使います。
シャミアの秘密分散は2つのステップに分かれます: シェアの計算とシークレットの復号です。一つずつ見ていきましょう。
シェアの計算
ステップ1: シークレットを決める
まず最初にシークレットを決めます。説明を簡単にするために、ここではとてもシンプルなシークレットにしましょう。3という数字をシークレットにします。
もちろんもっと複雑なシークレット、I love you とか 4b0649b1faf1c1ea7cb0e900 とかでも構いません。その場合は、数字として扱う必要があるので文字列をバイト配列に変換すればいいだけです。
ステップ2: 閾値を決める
次に閾値を決めます。ここでは 3 を閾値にしましょう。閾値が3なのでシークレットを復元するために三つシークレットが必要ということになります。
ステップ3: 多項式を生成する
シェアを計算するための多項式を生成します。多項式とはy=3x+1 や y=5x2+10x-3の形をした方程式のことです。 多項式の係数は自由に決めて構いませんが、次数は閾値 - 1じゃないといけません。
今回は閾値を3に設定したので、次数は2になります。次数が2の多項式はy=ax2+bx+cの形を取ります。係数はなんでもいいのでaは2、bは1にしましょう。
cにはシークレットを使わないといけません。つまり、cは3ということになります。
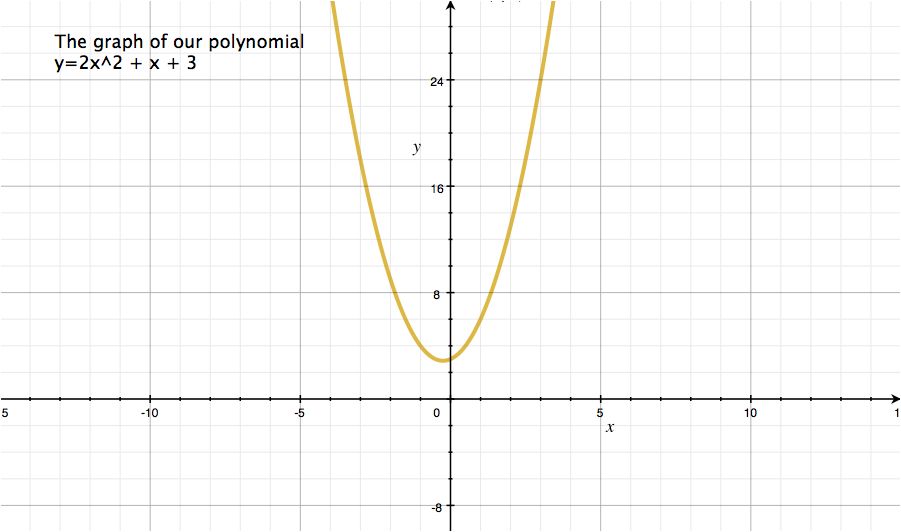
これで多項式ができました: y=2x2+x+3
準備は整いました。以下は上記の設定をまとめたものです。
シークレット: 3
閾値: 3
多項式: y=2x2+x+3
ステップ4: グラフを書く
このステップはシャミアの秘密分散の計算をするためには必ずしも必要ではありませんが、グラフを書くことで理解が簡単になります。
多項式のグラフは以下のようになります。
ステップ5: 点をグラフに描画する
三つの点をグラフの線上に書きます。
例として、(x,y)(1, 6), (x,y)(2,13), (x,y)(-2, 9)をグラフ線上に書いてみましょう。
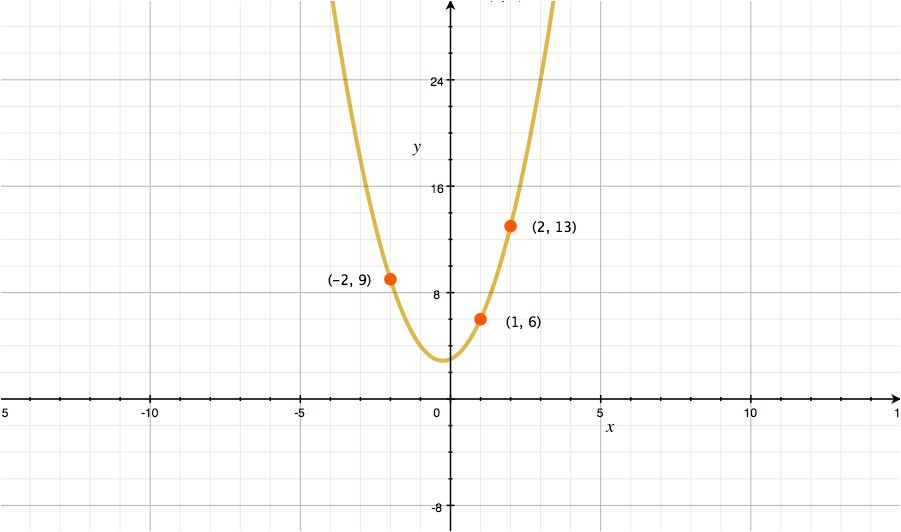
このそれぞれの点がシェアになります。xの値が前述したシェア番号になりyの値がシェアになります。
閾値を3に設定したことを思い出してください。閾値が3なので、今回は三つの点を書きました。
もっとシェアが必要であればさらに点を増やせばいいだけです。
シェアが計算できたら、シェアと閾値以外はすべて忘れて構いません。多項式、グラフ、シークレットは捨ててしまいましょう。
シェアと閾値を知っている限り他のすべてを復元することができます。
シークレットの復元
今、シェアと閾値以外は何も知らない状態ですが、ここから元のシークレットを復元することができます。
わかりやすくするためにもう一度グラフを使いましょう。
(x,y)(1, 6), (x,y)(2,13), (x,y)(-2, 9) の点をグラフに書きます。
次に、これらの点を線で結びます。これらの点は元の多項式から得た点なので線で結べばグラフを引くことができます。
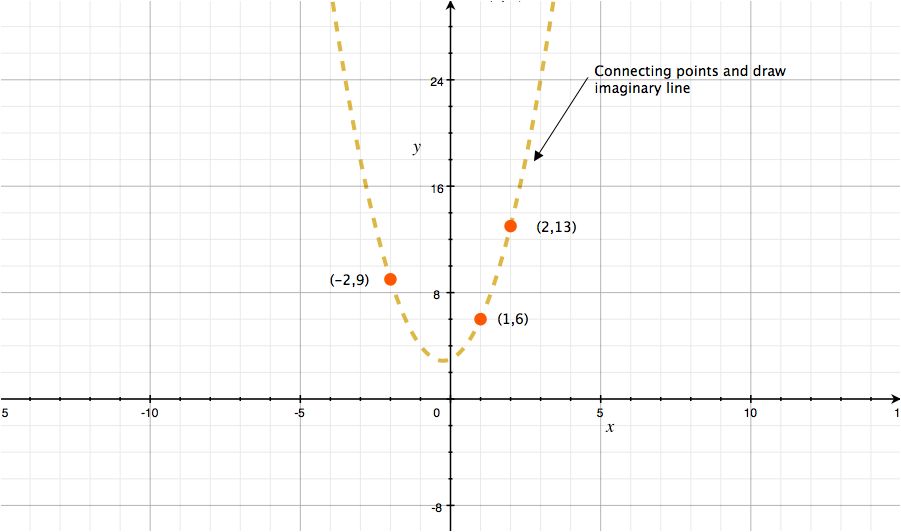
グラフはあくまで理解の助けをするためなので正確なグラフが書けなくても構いません。
しかし、多項式の定義では直線には2点、放射線には3点さえあれば正確な線を引くことができます。 (Wikipedia)
これにより、たとえ手で正確なグラフを書くことができなくても計算すれば正確なグラフを求めることができます。
多項式補間
閾値は3と知っているので、次数が2 (次数は閾値 - 1) のy=ax2+bx+cの形の多項式に点を代入すれば元の多項式を得ることができます。
3つの点をy=ax2+bx+cに代入します。
(1) (1,6) => c = a + b - 6
(2) (2,13) => c = 4a + 2b - 13
(3) (-2,9) => c = 4a - 2b - 9
次に(1)を(2)と(3)に代入してaを得ます。
(4) (1)を(2)に代入します => b = -3a + 7
(5) (1)を(3)に代入します => 3b = 3a -3
(6) (4)を(5)に代入します => a = 2
これで、aを得ることができました。今度はbを求めます。
(7) a=2を(1)に代入します => c=b - 4
(8) a=2を(2)に代入します => c=2b - 5
(9) (7)を(8)に代入します => b = 1
これでaとbを得ることができました。最後にcを得ます。
(10) a=2とb=1を(1)に代入します => c=3
これで終わりです。無事元の多項式であるy=2x2+x+3を得ることができました。係数がない項がシークレットなので正しいシークレットである3を復元することができました。