Divide And Manage Secret Data Securely With Shamir’s Secret Sharing

Recently, I came to know an interesting and new idea about password storage schema called PollyPassHash.

I may write about PolyPassHasing in more details in separate post, but in summary, PolyPassHashing proposes a new password storage schema that requires certain numbers of shared keys to decrypt the encrypted password.

In this post, I will write about Shamir’s secret sharing, one of key technologies used in PolyPassHashing, and try to explain the mathematical basis that archive this great secret sharing technology.

Contents of This Article

Basic terms

HandsOn: Play Shamir’s Secret with Ruby

As the name implies, Shamir’s secret sharing is created by Adi Shamir, an famous Israeli cryptographer, who also contributed to the invention of RSA algorithm.

Shamir’s secret sharing is an algorithm that divides a secret into shares. Secret can be recovered by combining certain numbers of shares.

Imagine a case where you have to encrypt some data. No matter which encryption method you use, you must store the secret key used in the encryption in order to decrypt later.

The key has to be very secured. If the key is stolen by attacker, your data will be easily decrypted. However, storing key is always difficult problem. It gets even more difficult if you need to share the key with others.

This problem of storing and sharing secret key is cause of headache for administrators.

However, if you use Shamir’s secret sharing algorithm, you can solve the two problems to greater extent.

You can divide your secret key into pieces and distribute them to other administrators. Each administrator still needs to keep a piece of secret key, but knowing a piece is not enough to recover the original secret.

Because attacker must compromise multiple administrator’s pieces, secret generated by Shamir’s secret sharing is very difficult to be compromised.

Basic Terms

Before going into details, let’s clarify some terms used in Shamir’s Secret sharing.

Secret

Secret is a secret message or number that you want to share with others securely.

Share is a piece of secret. Secret is divided into pieces and each piece is called share. It is computed from given secret. In order to recover the secret, you need to get certain numbers of shares.

Threshold

Threshold is the number of shares you need at least in order to recover your secret. You can restore your secret only when you have more than or equal to the number of threshold.

HandsOn: Play Shamir’s Secret With Ruby

Do you want to see what you can do with Shamir’s secret sharing? Let’s use a small Ruby library that I wrote to demonstrate the idea. This library is ported from Python Shamir’s secret sharing library used in PolyPassHash project originally written by JustinCappos.

First get the code from PolyPassHash-Ruby and load shamirsecret.rb into your irb session.

$ git clone https://github.com/PolyPassHash/PolyPassHash-Ruby
$ cd PolyPassHash-Ruby
$ irb -r ./shamirsecret.rb

Let’s encrypt some messages and see if we can recover the message when giving enough numbers of shares.

# First, you need to instantiate ShamirSecret class.
# You can specify the number of threshold in the first argument. In this case, two shares are required.
# You can pass a message to encrypt in the second argument.
shamirsecret = ShamirSecret.new(2, "In the name of Adi Shamir")

# We compute shares from the given secret. Let's assume we want to distribute to three parties, so lets create three shares.
# The argument is so called share number. You will know what it is later in this post.
# For now, just remember that it has to be unique number.
s1 = shamirsecret.compute_share(1)
s2 = shamirsecret.compute_share(2)
s3 = shamirsecret.compute_share(3)

# Once we computed shares, we will throw the secret away because we should be able to recover from shares.
shamirsecret = nil

# Then we will recover the secret. Instantiate ShamirSecret again. We don't pass secret this time because we just want to recover secret.
shamirsecret = ShamirSecret.new(2)

# Now we can recover the secret by giving two shares or more since we set threshold to be 2.
shamirsecret.recover_secretdata([s1,s3])
=> "In the name of Adi Shamir"

Let’s confirm what happens if we gave wrong shares.

# Instantiate and compute share in the same way
shamirsecret = ShamirSecret.new(2, "In the name of Adi Shamir")
s1 = shamirsecret.compute_share(1)
s2 = shamirsecret.compute_share(2)
s3 = shamirsecret.compute_share(3)

# Make sure our share is valid
shamirsecret.is_valid_share(s1)
=> true

# Change a byte of share
s1[1][0] = s1[1][0] + 1 % 256

# The share is not valid anymore
shamirsecret.is_valid_share(s1)
=> false

# Secret is corrupted with wrong share
shamirsecret = nil
shamirsecret = ShamirSecret.new(2)
shamirsecret.recover_secretdata([s1,s3])
=> "\xC6n the name of Adi Shamir"

How This Works

It’s time to do some math. Shamir’s secret sharing is using the very basic idea of polynomial.

We have two major steps: Share Computation and Secret Reconstruction. Let’s do one by one.

Step1: Decide secret

First, we need to decide our secret message. To make our story simple, let’s choose dead simple one, 3, as our secret.

If you choose more complex message such as I love you or 4b0649b1faf1c1ea7cb0e900, you just need to convert them to byte array so that you can treat them as a number.

Step2: Decide threshold

Next thing to decide is the threshold. We will choose 3 as our threshold. This means that you need at least three shares to recover the secret.

Step3: Create polynomial

We need to create our polynomial. Polynomial is the equation that looks like y=3x+1 or y=5x²+10x-3. You can choose any numbers for coefficient, but the degree of your polynomial must be **threshold -1 **.

Our threshold is 3, so the degree must be 2 in our case. The polynomial of degree of 2 should takes the form of y=ax²+bx+c. Since you can choose any numbers for coefficient, we will use 2 for a and 1 for b.

What c will be? c must to be our secret. Therefore, we use 3 for c.

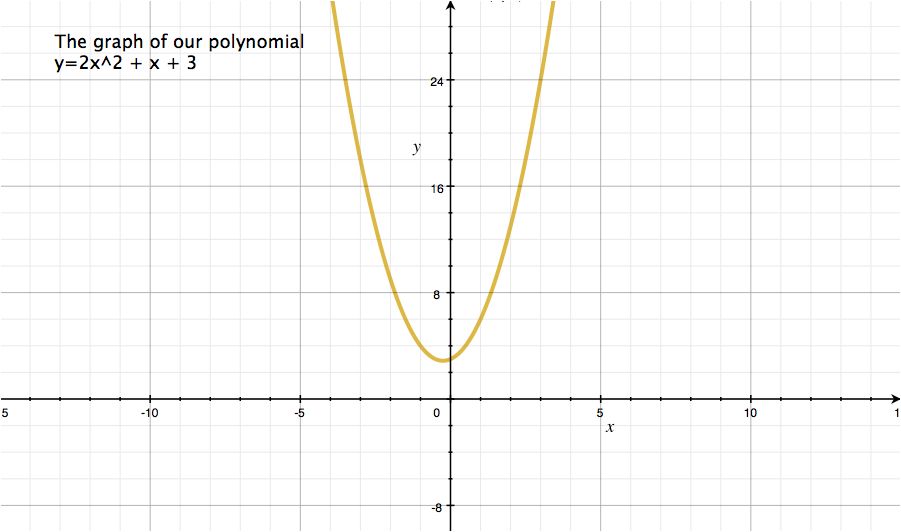
This is our polynomial: y=2x²+x+3.

Now we have everything to demonstrate Shamir’s secret sharing. This is our configuration

Secret: 3

Threshold: 3

Polynomial: y=2x²+x+3

Step4: Draw graph

Note that drawing graph is not necessary to do computation for Shamir’s secret sharing. However, we can understand how this works better by drawing graph.

The graph of our polynomial looks like this one.

Graph of y=2x^2+x+3

Step5: Plot points on the graph

Plot three points on the line of graph.

For example, we plot (x,y)(1, 6), (x,y)(2,13), (x,y)(-2, 9) on the line of graph.

Plot points on the line of graph

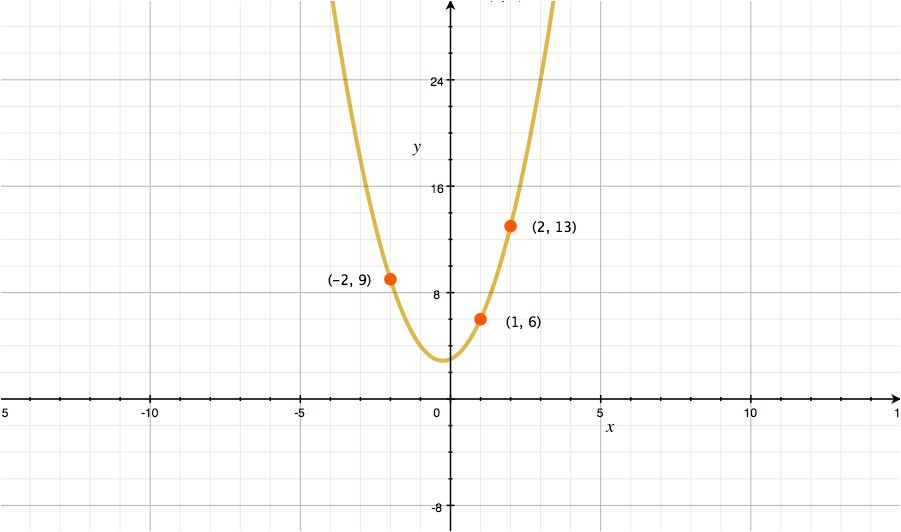
These points are your shares. The value in x is called share number and the value of y is a share.

Remember that we decided our threshold to be 3? Three shares are minimum number of shares that we need. That’s why we plotted three points.

You can get even more shares by plotting extra points if you want to distribute shares to more parties.

Once you get shares, forget everything but your threshold and shares!! Throw your polynomial, the graph, and your secret.

As long as you have your shares and threshold, you can recover everything else.

Secret Reconstruction

Now you know nothing but shares and threshold, but you can still recover your secret by combining the shares.

To get this idea, we will again use graph.

Plot points of your shares, (x,y)(1, 6), (x,y)(2,13), (x,y)(-2, 9), on the graph. Then connecting your points and draw imaginary line. If you could do this, you can now recover your polynomial because you are connecting points derived from the polynomial.

Not sure if your line is accurate? Yes, it is is difficult to draw the completely same line because it is curving line. It doesn’t matter because drawing graph is just to help you understand the idea.

However, by definition, 2 points are sufficient to define a line, 3 points are sufficient to define a parabola (Wikipedia)

Therefore, although it is difficult to draw the imaginary line by hands from points of shares, you should be able to do that by doing some math. Now, let’s do this.

Polynomial interpolation

Since we know that our threshold is 3, we know that we need to get the polynomial of degree of 2 (remember that degree is threshold - 1) which looks like this: y=ax²+bx+c

Substitute three points into y=ax²+bx+c.

(1) (1,6) => c = a + b - 6

(2) (2,13) => c = 4a + 2b - 13

(3) (-2,9) => c = 4a - 2b - 9

Now substitute (1) into (2) and (3) to get a.

(4) substitute (1) into (2) => b = -3a + 7

(5) substitute (1) into (3) => 3b = 3a -3

(6) substitute (4) into (5) => a = 2

We could get a. Let’s compute b next.

(7) substitute a=2 into (1) => c=b - 4

(8) substitute a=2 into (2) => c=2b - 5

(9) substitute (7) into (8) => b = 1

Now we could get a and b. At last, we can compute c.

(10) substitute a=2 and b=1 into (1) => c=3

We are done. We could recover original polynomial y=2x²+x+3 and you can find your secret at free coefficient, which is 3.